Jim Frankenfield - Papers[Technical] [Administrative] [Avalanche] [Web] |
[Papers] 
|
Volumes and areas of pendular rings with non-zero contact angles
Jim Frankenfield; 1338 Foothill Drive; Salt Lake City, UT 84108, USA
877-604-0166; snowman@csac.org
Copyright Notice
This paper was originally accepted to appear in Water Resources Research until another individual attempted to take credit for much of the work. As a result I withdrew the paper and filed an official copyright claim.
Abstract
The geometric configuration of the wetting and nonwetting fluids in the pendular regime of saturation in a porous medium has direct bearing on the physical state of the fluid. It is of practical interest in petroleum, chemical and environmental engineering, and other fields. Previously published expressions for the volume of pendular rings in an ideal medium having zero contact angle are reviewed, compared, and found to be in disagreement. The only published volume expression for pendular rings of fluid with non-zero contact angle is found to be incorrect, and a new general expression is derived and verified. A singularity in this expression is addressed. New general volume and area expressions for two variations from an ideal medium are presented. The effect of contact angle on the maximum size of a pendular ring is discussed and the effect on wetting fluid saturation in an ideal medium is demonstrated.
Introduction
Pendular configurations of wetting fluids in multiphase saturated porous media are of interest as a fundamental issue in hydrostatics, and from a practical point of view in petroleum and environmental engineering as well as other fields involving fluid behavior in porous media. Packings of spheres are commonly used to model sands and sandstones found in nature [Rose, 1958]. Knowledge of the volumes of the pendular rings would allow better estimates of oil reserves expressed as a fraction of pore-space saturation. Other areas of application include groundwater remediation and bioremediation [Atlas, 1988] and the mechanics and thermodynamics of wet snow [Denoth, 1982] [Brun and Rey, 1987]. Figure 1 shows a pendular ring of wetting fluid about the point of contact of two identical spherical particles. Such a configuration has also been referred to as a capillary ring and as a meniscus.
There is a large body of work addressing the precise shape of the fluid-fluid interface, most of which does not lead to explicit expressions for volume or surface area. Smith et al. [1930], assuming that the curvature of the fluid-fluid interface obeys Plateau�s equation, were able to obtain a volume expression for the case of a zero contact angle between the wetting fluid and the solid particle. Rose [1958] regarded all three surfaces of the ring as arcs of circles and compared the resulting volume expression to that of Smith et al [1930]. The two expressions were found to be in very close agreement. The assumption that all three surfaces are circular arcs was the basis for the expressions cited and derived in the following sections.
Additional assumptions are that the effects of gravity are negligible in relation to capillary forces and that the volume of any wetting fluid in a thin coating layer due to the hydrophilic properties of the solid is negligible compared to the volume found in the pendular rings. The first assumption applies for spheres less than 1 mm in radius [Smith et al., 1930] and the second applies for spheres greater that 10-3 mm in radius [Gvirtzman and Roberts, 1991].
Review of Previous Volume Results
The geometry of pendular rings in an ideal medium consisting of identical spherical particles in contact with each other has been investigated by several authors. The results are summarized here in a consistent notation.
Let the size of the pendular ring be denoted by theta and the contact angle between the wetting phase and the solid spherical particle of an ideal soil by phi. Define angle omega as (pi/2)- theta - phi. (Figure 1.)
A number of expressions for the volume of pendular rings have been presented in the literature. For the case of a zero contact angle the volume has been given by Rose [1958] as
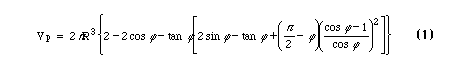
while Gardner and Gardner [1953] found
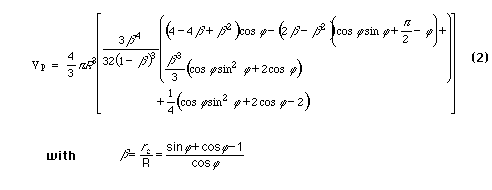
and without derivation Dallavalle [1948] reported that
![]()
For the case of a non-zero contact angle an expression for the volume of a pendular ring has been given by Gvirtzman and Roberts [1991] which, for zero contact angle, reduces to
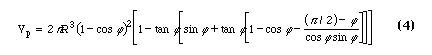
When the four expressions for zero contact angle are compared graphically discrepancies are apparent. The ratio of equation (1) to equation (2) is 2 for all theta. A review of the derivation of (2) shows that the result is for half of a ring. Higher volumes are predicted by (4) and lower volumes are predicted by (3), but these results are not related by a ratio which is constant or an easily recognizable function of theta. (Figure 2.) Use of (4) to calculate pendular wetting fluid saturation can result in values in excess of one hundred percent.
A General Volume Expression
An expression for the volume of a pendular ring which includes the possibility of non-zero contact angle is desired. Such an expression may be obtained by direct integration. By summing over annuli of thickness dy and volume dV (Figure 1), the integral
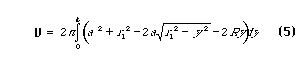
is obtained. Evaluation of this integral gives
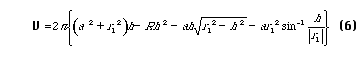
No assumptions concerning contact angle have been made thus far.
If (6) is simplified for the zero contact angle case the result is identical to (1), verifying the result of Rose1. For the case of non-zero contact angle simplification yields
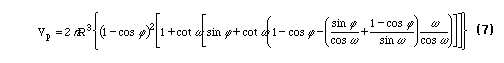
The effect of a non-zero contact angle on the volume of the pendular ring is shown in Figure 3.
Equation (7) has a singularity when w = 0, which occurs when theta + phi = pi/2. This can happen, for example, when the contact angle is 50 degrees and the ring size is 40 degrees. If (7) is rewritten as a single fraction and l'hopitals rule is applied three times, it is found that
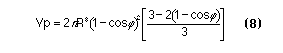
These points lie on the volume curve and are included in Figure 3.
Area Expressions
The discrepancies which have plagued the issue of wetting fluid volume are not found when it comes to the areas of the interfaces. The following expressions have been verified as correct, and are included here to provide a complete set of correct expressions in a consistent notation.
The area of the interface between the wetting and nonwetting fluids, for the general case of a non-zero contact angle, was given by Gvirtzman and Roberts [1991] as
![]()
For the case of a zero contact angle this reduces to the expression given by Rose [1958],
![]()
The area of the interface between the wetting fluid and the one of the solid particles is part of a sphere,
![]()
Variations From an Ideal Medium
There are a few variations from the ideal medium which are of interest. Two identical spheres which are not in contact with each other but separated by a small enough distance d can support a pendular ring between them (Figure 4). The volume and area of such a ring can be derived in the same manner as the ideal case. The volume is
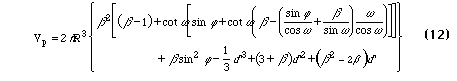
and the area is
![]()
where beta = 1 - cos(theta) + d' and d' = d/(2R).
Another case of interest is when the contact between the spheres is flattened, as if they overlapped. This type of contact between spheres can be used to approximate snow or ice grains which have sintered together [Colbeck, 1979]. Let a be the angle denoting the size of the circular flattened contact area. (Figure 5.) The volume is
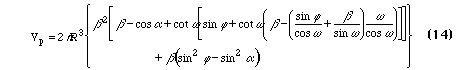
and the area is
![]()
where beta = cos(alpha) - cos(theta).
These expressions all reduce to the ideal medium case in the appropriate limit (alpha or d approaching zero). The effect of separation d and flattening a on ring volume are demonstrated in Figure 6.
The case of a ring with zero contact angle between two spheres of different sizes was addressed by Rose [1958]. The result was quite lengthy and was left in terms of many variables, even for this special case.
Effect of Contact Angle on Maximum Ring Size
When the pressure difference across the wetting-nonwetting interface becomes zero the rings can not become any larger. This pressure is given by the Laplace equation,
![]()
where gwn is the interfacial tension between the wetting and nonwetting fluids, so that r1 = r2 gives a condition for maximum ring size. Using Figure 1, Figure 4, and Figure 5, this condition can be expressed in terms of ring size theta and contact angle phi;
![]()
where beta = 1-cos(theta) for the ideal medium case, beta = 1-cos(theta)+d' for separated particles, and beta = cos(alpha) - cos(theta) for the flattened contact.
A good approximation in the ideal case is
![]()
Figure 7 shows the dependence of maximum ring size on contact angle.
When the solid spheres are separated by some distance d equation (17) can also be used to examine the maximum distance d possible for a given contact angle and the maximum ring size for given values of contact angle and separation d. Figure 8 demonstrates the nature of these relationships.
Effect of Contact Angle on Saturation in an Ideal Medium
For a packing of spheres the saturation can be calculated as the ratio of the volume of the rings of wetting fluid contained in a unit cell to the volume of pore space in a unit cell. For an ideal medium the resulting expression was given by Gvirtzman and Roberts [1991] and is
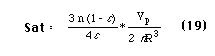
where epsilon is the porosity and n is the number of spheres which each sphere touches, and is called the grain coordination number. The limiting cases of rhombohedral (closest) packing and cubic (open) packing can be used to examine the effect of contact angle on saturation.
In a packing of sheres the maximum ring size will be determined by one of two factors. When the ring size (theta) is equal to half the packing angle the rings will merge (i.e. at 30 degrees in a rhombic packing and at 45 degrees in a cubic packing.) However, if the pressure difference across the wetting-nonwetting interface becomes zero before they merge the rings will not become any larger, as discussed in the previous section.
Saturation as a function of ring size for a rhombic packing is shown for three different contact angles in Figure 9. In a rhombic packing of spheres porosity (epsilon) is 0.2595 and the grain coordination number (n) is 12. For contact angles of less than 43.8 degrees the maximum ring size based on the pressure criteria is greater than 30 degrees, so for the three cases shown the rings will grow until they merge. The error incurred in calculations of the wetting fluid volume if the contact angle was neglected (assumed to be zero) would be 6.7 percent of the total pore space for a contact angle of 20 degrees and 12.3 percent for a contact angle of 40 degrees.
Figure 10 shows saturation as a function of ring size for a cubic packing. In this packing porosity (epsilon) is .4764 and the grain coordination number (n) is 6. For contact angles of less than 17.5 degrees the maximum ring size based on the pressure criteria is greater than 45 degrees and the rings will grow until they merge. However, for contact angles greater than 17.5 degrees the fluid will become nonpendular at some angle less than 45 degrees due to the pressure criteria. Note that neglecting the contact angle in this case may result in either an overestimate or an underestimate of the wetting fluid volume. The error for the cases shown is 3.5 percent of total pore space for a contact angle of 20 degrees and -10.2 percent (an overestimate) for a contact angle of 40 degrees.
Discussion and Conclusion
Four expressions for the volume of pendular rings with zero contact angle which have been published over the last forty six years were identified and compared graphically. It was found that they are not in agreement. A general expression for the volume of a pendular ring was derived and singularities in it were addressed. For the case of zero contact angle it can be reduced to the expression given by Rose [1958]. Correct area expressions were summarized. Volume and area expressions were presented for the non-ideal cases of separated particles and flattened areas of contact. The new volume expressions were used to demonstrate the effect of a non-zero contact angle. The effect on maximum ring size was addressed for all three cases. The effect of contact angle on wetting fluid saturation (as a percent of pore space) in an ideal medium was shown and discussed. If contact angle is neglected (assumed zero) errors of 12 percent or more of total pore space are possible, and can be manifest as either over or under estimates.
References
Atlas, R.M., in Environmental Biotechnology, edited by G.S. Omenn), pp 211-222, Plenum, New York, 1988.
Brun, E. and L. Rey, IAHS Publication No 162, pp 183-184, IAHS, 1987.
Colbeck, S.C., J. Colloid Interface Sci. 72, p. 371 (1979)
Dallavalle, J.M., in Micromeritics, 2nd ed., p. 288, Pittman, 1948.
Denoth, A., Journal of Glaciology 28, 357 (1982).
Gardner, Willard and John Hale Gardner, Soil Sci. 76, p. 135 (1953).
Gvirtzman, Haim and Paul V. Roberts, Water Resour. Res. 27, p 1167 (1991).
Rose, Walter, J. Appl. Phys. 29, p 687 (1958).
Smith, Foote and Busang, Phys. Rev. 36, p 524 (1930)
Index to Figures, with Captions
Figure 1 - Cross section of a pendular ring of wetting fluid surrounding the point of contact of two identical spherical particles, with parameters defined.
Figure 2 - Scaled volume (Vp/2pR3) as a function of ring size for previously published zero contact angle expressions. (Top to Bottom: Gvirtzman and Roberts, Rose, Dallavalle, Gardner.)
Figure 3 - Scaled volume (Vp/2pR3) vs. ring size for three different contact angles (Top to Bottom: 40 degrees, 20 degrees, 0 degrees.) Square points mark limits at the singularity.
Figure 4 - Cross section of a pendular ring of wetting fluid between two identical spherical particles separated by a distance d.
Figure 5 - Cross section of a pendular ring of wetting fluid between two identical spherical particles which have a flattened area of contact. Detail follows from Figure 1 and Figure 4.
Figure 6 - Effect of separation distance d' or flattened contact angle a on the volume of a pendular ring when contact angle is 20 degrees. The top solid line is the ideal case, the other solid line is for a=20, and the dashed line is for d'=0.1
Figure 7 - Maximum ring size in degrees as a function of contact angle. The solid line in the middle is the ideal case, the top line is for a=20, and the lowest line is for d'=0.05
Figure 8 - Maximum separation of the solid spheres as a function of contact angle (solid line) and maximum pendular ring size as a function of separation for a zero contact angle (dashed line).
Figure 9 - Effect of contact angle on saturation in a rhombic packing. (Contact Angles, from Top to Bottom: 40 degrees, 20 degrees, 0 degrees.)
Figure 10 - Effect of contact angle on saturation in a cubic packing (Contact Angles, from Top to Bottom: 40 degrees, 20 degrees, 0 degrees)

 Jim Frankenfield. |
[Papers] 
|